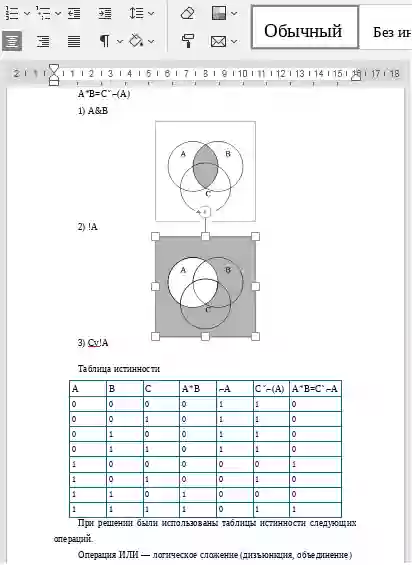
Диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств.Чтобы нарисовать диаграммы по формуле, используйте данный сервис. Если требуется создать круги с различным оформлением, используйте этот калькулятор.
(...) - задание скобок; A - отрицание, инверсия, дополнение (NOT); ∪ - дизъюнкция, объединение (OR); ∩ - конъюнкция, пересечение (AND); = - эквивалентность (тождество) (↔); → - импликация (следование); \ - относительное дополнение (разность); △ - симметрическая разность.
Для вложенного отрицания необходимо использовать знак !. Например, A ∪ B = !(A ∪ B) или A ∪ B = A ∪ !B
Чтобы доказать равенство, например,
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр
Чтобы доказать равенство, например,
(A\B)\C∩B = (A\C)\(B\C), необходимо отдельно ввести (A\B)\C∩B и (A\C)\(B\C), а затем сравнить их результаты.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр
Упростить выражение).
Здесь будет показано решение
Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).
Универсальное множество (универсум) U - множество, содержащее все элементы рассматриваемых подмножеств и элементы, не входящие в них.Пустое множество Ø - множество, не содержащее ни одного элемента рассматриваемых подмножеств.
Количество пересечений (областей) n определяется по формуле:
n=2N,
где N - количество множеств.
Рисование кругов Эйлера
С помощью этого инструмента можно будет вручную создавать круги Венна с индивидуальным оформлением. Чтобы заштриховать требуемую область, нажмите на кнопку Заштриховать область, а затем выберите номер области. Для снятия штриховки, повторно нажмите на этот же номер.
Количество переменных (кругов)
Оформление кругов
Цвет линии
Цвет штриховки
Использовать сетку
Для закрашенной области можно получить ее соответствующее описание через логические операции.
Алгоритм построения диаграмм Эйлера-Венна
- Определяют количество подмножеств (А, В, С, D).
- На диаграмме строят пересекающиеся множества, включенных в универсум.
- Выделяют области, количество которых равно количеству пересечений.
Диаграммы Эйлера-Венна для одного множества А
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=21 = 2 строк (областей)
Примеры
Универсум U={0,1,2,3}, А={2,4}
A = {0,1,3}, A ∩ A = {2,4}∩{0,1,3} = {} = Ø
Диаграммы Эйлера-Венна для двух множеств А и В
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=22 = 4 строк (областей)
Примеры
Универсум U={0,1,2,3,4,5}, А={0,3,4}, В={3,4,5}
A∪B = {0,3,4} ∪ {3,4,5} = {0,3,4,5}
Диаграммы Эйлера-Венна для трех множеств А, В, С
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=23 = 8 строк (областей)
Примеры
Универсум U={0,1,2,3,4,5}, А={2}, В={3,4,5}, C={3,4}
B\C ∪ A = {3,4,5}\{3,4} ∪ {2} = {5} ∪ {2} = {2,5}
Диаграммы Эйлера-Венна для четырех множеств А, В, С, D
На последнем рисунке приведены соответствующие области таблицы истинности, которая состоит из n=24 = 16 строк (областей)
Примеры
Универсум U={0,1,2,3,4,5}
А={1,2,3,4}
В={3}
C={4}
D={0}
Логические операции
Для описания логических операций можно использовать круги Эйлера и таблицы истинности.| Логическая операция | Обозначение | Диаграмма Эйлера-Венна |
инверсия (отрицание, логическое не, дополнение) | !, ¬ | |
конъюнкция (логическое и) | AND, &, ∩, ∧ | |
дизъюнкция (логическое или) | OR, ∪ +, ∨ | |
| импликация (следование) A→B = A∪B | → | |
| эквивалентность (тождество) A↔B = (A∩B)∪(A∩B) | =, ↔ | |
| относительное дополнение (разность) A\B = A∩B | - , \ | |
| симметрическая разность A△B = A∩B ∪ A∩B | △, XOR |
Список литературы
- Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
- Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
- Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.